Note: please see the 2021 update to this post, here.

In games and graphics one often needs to generate pseudorandom numbers. Needless to say, PRNGs are an extremely well-researched topic; however, the majority of the literature focuses on applications with very exacting quality requirements: cryptography, high-dimensional Monte Carlo simulations, and suchlike. These PRNGs tend to have hundreds of bytes of state and take hundreds of instructions to update. That’s way overkill for many more modest purposes—if you just want to do a little random sampling in a game context, you can probably get away with much less.

To drive home just how much lower my random number standards will be for this article, I’m not going to run a single statistical test on the numbers I generate—I’m just going to look at them! The human visual system is pretty good at picking out patterns in what we see, so if we generate a bitmap with one random bit per pixel, black or white, it’s easy to see if we’re generating “pretty random” numbers—or if something’s going wrong.

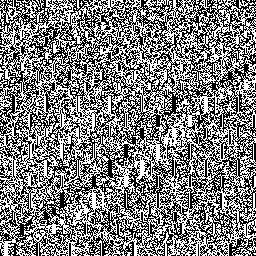
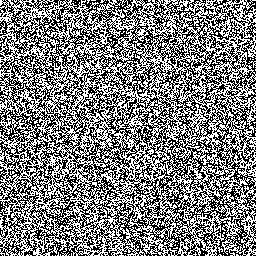
The one on the left is a linear congruential generator (LCG), and on the right is Xorshift. We’re always told that LCGs are bad news, and now you can see just how bad! Xorshift, on the other hand, is much better. It’ll actually pass some medium-strength statistical tests, and it certainly looks random enough to the eye. Moreover, it’s quite fast compared to other PRNGs of similar quality.

Since D3D11 GPUs support integer operations natively, it’s easy to port these PRNGs to shader code. GPUs do things in parallel, so we’ll create an independent instance of the PRNG for each work item—vertex, pixel, or compute-shader thread. Then we just need to seed them with different values, e.g. using the vertex index, pixel screen coordinates, or thread index, and we’ll get different sequences. Here’s the shader code for the LCG and Xorshift versions I used:

uint rng_state;

uint rand_lcg()
{
    // LCG values from Numerical Recipes
    rng_state = 1664525 * rng_state + 1013904223;
    return rng_state;
}

uint rand_xorshift()
{
    // Xorshift algorithm from George Marsaglia's paper
    rng_state ^= (rng_state << 13);
    rng_state ^= (rng_state >> 17);
    rng_state ^= (rng_state << 5);
    return rng_state;
}

// Example of using Xorshift in a compute shader
[numthreads(256, 1, 1)]
void cs_main(uint3 threadId : SV_DispatchThreadID)
{
    // Seed the PRNG using the thread ID
    rng_state = threadId.x;

    // Generate a few numbers...
    uint r0 = rand_xorshift();
    uint r1 = rand_xorshift();
    // Do some stuff with them...

    // Generate a random float in [0, 1)...
    float f0 = float(rand_xorshift()) * (1.0 / 4294967296.0);

    // ...etc.
}

LCGs are really fast—updating the state takes just one imad instruction (in HLSL assembly, which is just an intermediate language, but still a reasonable proxy for machine code speed). Xorshift is a bit slower, requiring six instructions, but that’s not bad considering the quality of random numbers it gives you. Figure two or three more instructions to get the number into the range you need, and convert it to a float if necessary. On a high-end GPU, you can generate tens of billions of random numbers per second with these PRNGs, easy.

However, running the PRNGs in parallel this way, generating a bitmap with one 32-bit word from each thread gives an unexpected result:

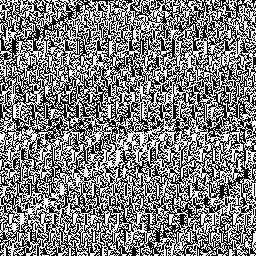
Again, on the left is the LCG and on the right is Xorshift. The LCG doesn’t look too different from before, but Xorshift looks absolutely terrible! What’s going on?

Wide and Deep

PRNGs are designed to be well-distributed when you “go deep”—draw many values from the same instance. Since this involves sequentially updating the state after each value, it doesn’t map well to the GPU. On the GPU we need to “go wide”—set up a lot of independent PRNG instances with different seeds so we can draw from each of them in parallel. But PRNGs aren’t designed to give good statistics across seeds. I tried several small PRNGs I found on the Web, and they all produced obvious artifacts when going wide, even if they were perfectly fine going deep.

The first thing I tried to fix this problem was to just throw away the first few values of each PRNG sequence, hoping the unwanted correlation would disappear after a few iterations. However, this doesn’t help much—once the sequences are correlated, they tend to stay that way. Here are the LCG and Xorshift after 64 iterations per thread:

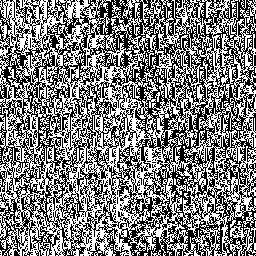
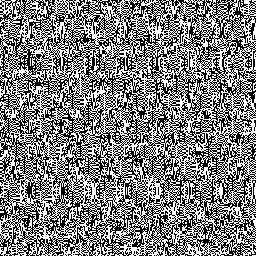
It’s better, but there are still pretty obvious nonrandom patterns, even 64 iterations deep into each sequence.

We need another ingredient. Fortunately, there’s another kind of pseudorandom function that’s explicitly designed to be well-distributed when going wide: hash functions. If we hash the seed when initializing the PRNG, it should mix things up enough to decorrelate the sequences of nearby threads.

(Incidentally, I was confused for a long time about the distinction between PRNGs and hash functions—they seem to do the same thing, i.e. create an “unpredictable” but deterministic output by jumbling up input bits. It wasn’t until I started playing around with GPU PRNGs that I realized the difference: PRNGs are designed for going deep, and hashes for going wide.)

Researching hash functions on the Web presents a similar problem to researching PRNGs: most of the ones you hear about are crypto hashes, or hashes designed to digest large and variable-length data, and many produce a 64-bit or 128-bit output. For initializing a PRNG, we just want something that can hash one 32-bit integer into another. The fastest hash function I’ve found that fits the bill is one invented by Thomas Wang, as reported on Bob Jenkins’ website. The Wang hash goes as follows:

uint wang_hash(uint seed)
{
    seed = (seed ^ 61) ^ (seed >> 16);
    seed *= 9;
    seed = seed ^ (seed >> 4);
    seed *= 0x27d4eb2d;
    seed = seed ^ (seed >> 15);
    return seed;
}

It’s nine instructions in HLSL assembly, and does a fine job of randomizing the seeds. Here’s the output of the Wang hash, using thread index as a seed, without any additional PRNG iterations:

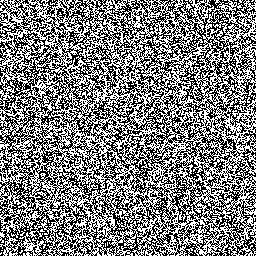
To the eye, it’s indistinguishable from true randomness. In fact, we could just iterate the Wang hash and it would make a perfectly good PRNG. However, it’s a few more instructions than Xorshift or the LCG, so it’ll be a little slower. It makes more sense to use the hash as a high-power tool to obliterate any correlation in the seeds, then turn things over to one of the PRNGs.

To sum up: if you need quick and easy GPU random numbers and don’t have stringent statistical requirements, I recommend either an LCG (faster) or Xorshift (better distributed when going deep), seeded using the Wang hash in either case. These are both great choices that are quite fast and will most likely give results plenty good enough for games and graphics applications.

Update 2021/05/21: I no longer recommend Xorshift or the Wang hash; based on newer research, it appears PCG is a better choice overall for GPU random number generation. See my updated article for more.