One of the key ingredients of a microfacet BRDF is its normal distribution function (NDF), which statistically describes the microscopic shape of the surface as a distribution of microfacet orientations. For an NDF to be physically sensible it should satisfy certain conditions, such as normalization. But the correct way to normalize an NDF isn’t what you might intuitively think, and I’d like to explain why.

An NDF is a function that gives, loosely speaking, the “likelihood” of a microfacet being aligned in a particular direction. In the BRDF it serves as a weighting function to scale the brightness of reflections, but the NDF is fundamentally a geometric property of the surface, and we should be able to understand it in such terms, without reference to light scattering.

Since it’s a function of direction, and it has units of inverse solid angle, it seems natural to think of the NDF as a probability density over solid angle. Formally, if we have a direction (unit vector) $h$ in the normal hemisphere, and a small piece of solid angle $d\omega_h$ representing a set of directions near $h$, then the probability of a microfacet having a normal within $d\omega_h$ is $D(h)\,d\omega_h$, where $D(h)$ is the NDF.

Since the probability of the microfacet normal being somewhere in the normal hemisphere should be 100%, the integral of the NDF over the whole normal hemisphere should be 1: $$\int_\Omega D(h) \, d\omega_h = 1$$ Seems simple enough, right? Except it’s wrong! If you take a standard NDF, such as the Blinn-Phong, Beckmann or GGX distribution, and plug it into the above integral, the result will not in general be 1. For example, with the Beckmann distribution and $m = 0.5$, the integral above comes out to about 1.113. (Try it in your favorite computer algebra system! I’ll wait.)

It turns out that the correct condition for an NDF to be normalized is: $$\int_\Omega D(h) \, (n \cdot h) \, d\omega_h = 1$$ Again, you can try this with your favorite NDF and see that it comes out to 1 as it should.

If you’ve read much about BRDFs and radiometry, the extra $n \cdot h$ factor is probably screaming out “projected area” at you. Indeed it shows up as the conversion factor between macrosurface area, aligned with $n$, and microfacet area, aligned with $h$:

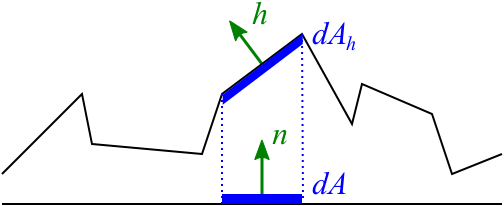
If $dA_h$ is a microfacet with normal $h$, and its projection onto the macrosurface is $dA$, then $dA = (n \cdot h) \, dA_h$.

So, it seems the NDF is not just a probability density over solid angle; it has something to do with area as well—in fact, two different area measures: macro-area and micro-area. So what is it really?

You Found a Secret Area!

The GGX paper, Microfacet Models for Refraction through Rough Surfaces by Walter et al., has the answer. According to them, the NDF obeys the equation: $$dA_h = D(h) \, d\omega_h \, A$$ where $A$ is a patch of macrosurface small enough to be considered flat, but much larger than an individual microfacet, and $dA_h$ is the total area of all the microfacets within $A$ that have normals within $d\omega_h$.

On this view, the NDF is not a probability density at all! Rather, it’s the density of micro-area over the joint domain of macro-area and solid angle. The area units cancel, so the NDF still has units of inverse solid angle, but the fact that it involves area is required to correctly understand and reason about it.

The normalization condition can then be derived from the above equation: after a bit of fiddling, we get $$\frac{1}{A} \int (n \cdot h) \, dA_h = \int_\Omega D(h) \, (n \cdot h) \, d\omega_h$$ The integral on the left is done over the area of all microfacets in the patch, and that on the right is done over the solid angle of the normal hemisphere. If we require this equation to equal 1, we’re saying that the total projected area of all the microfacets should equal the area of the macrosurface patch. In other words, there are exactly as many microfacets as needed to cover the macrosurface, without holes or overlaps. The normalization condition on the NDF ensures that it’s consistent with this picture.

Walter et al. give a stronger condition: for any direction $v$, we should have $$\int_\Omega D(h) \, (v \cdot h) \, d\omega_h = n \cdot v$$ The normalization condition follows from this in the special case $v = n$. The more general condition ensures that the NDF is consistent with the microsurface being manifold, not just a triangle soup. The microsurface’s boundaries must match those of the macrosurface.

(I’m not sure if it’s actually possible for an NDF to satisfy the normalization condition, but fail to satisfy the manifold condition for some other $v$. If you know a counterexample, please post it in the comments!)

Incidentally, I’ve assumed here that microfacet normals are always in the normal hemisphere, which—together with the manifold condition—forces the microsurface to be a heightfield. This is convenient, but not essential. For a general 3D microsurface, just extend all integrals from the hemisphere to the whole sphere. Note that all the dot products are unclamped, and that many standard NDFs like the Blinn-Phong, Beckmann and GGX distributions are zero in the antinormal hemisphere.

The fact that an NDF isn’t just a probability density of microfacet normals over solid angle, and that it needs an $n \cdot h$ in its normalization, doesn’t seem to be very well-known. It certainly had me confused for some time, and even Real-Time Rendering unfortunately gets this a bit wrong.