In a previous post, I wrote about using numerical integration to calculate how the universe expands over time. It turned out that dark energy is making the expansion of the universe speed up, and (we presume) it will continue to do so forever. The universe’s destiny is a runaway accelerating expansion! Moreover, the details of this destiny depend sensitively on the detailed behavior of dark energy—specifically, how its density changes as space expands.

Matter and radiation naturally thin out as the universe expands: there’s a finite amount of each, spread over an increasing volume of space, and no more is being created (although a little matter converts into radiation from time to time). But dark energy works differently. Observations have established that its density remains very close to constant—as the volume of space grows, more and more dark energy comes into existence! But what observation can’t yet answer is: does dark energy’s density remain exactly constant? Or does the expansion of space dilute it just a little? Or might dark energy perversely become slightly more concentrated as the universe grows?

The answer to this question has a huge effect on the far future of the universe. As we saw last time, the behavior of dark energy can be characterized by a numerical parameter called $w$, which we know to be equal to −1, to within about a 10% error, from current data.

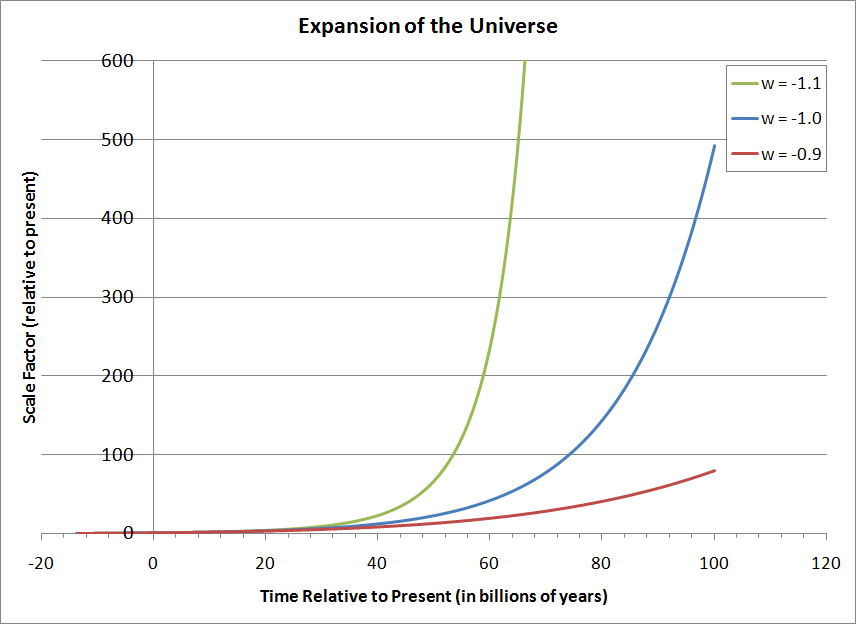
This graph shows the predicted expansion of the universe over the next 100 billion years under three scenarios. When $w = -1$ the density of dark energy is constant; when $w > -1$ it is diluted slightly by spatial expansion, and when $w < -1$ it is slightly concentrated by the expansion. (This last case requires some fairly exotic particle physics to implement, but there are models out there that can explain such behavior! See this paper’s references for some examples.) These curves show that the rate of expansion in the far future depends sensitively on $w$, but what you can’t see from the graph is that the curves are actually qualitatively different; they have different mathematical forms, with very different asymptotic behaviors.

One interesting way to see how these behaviors is to look at the behavior of the cosmic horizon. Much like a horizon here on Earth, the cosmic horizon marks the boundary of how far we can see into the universe. Also like a horizon on Earth, it’s observer-dependent—its presence and location depend on where you are (and, in relativity, your state of motion). It also depends on the global structure of space-time!

Why should there be a cosmic horizon at all? Well, for one thing, the universe is only finitely old and light travels finitely fast, so there are parts of space that we can’t see because light hasn’t had time to get here from there since the Big Bang. So there’s a notional sphere around us (or around any observer) that represents the farthest we can see, and it’s constantly expanding as time goes on and new light arrives from ever-farther locations. This is one example of a horizon, called by physicists the “particle horizon”. In a static, non-expanding universe, the particle horizon would grow without bound forever, and we’d eventually be able to see arbitrarily far.

However, in an expanding universe there’s another kind of horizon. It’s possible for an object to be so far away that light from it never reaches us, no matter how long we wait: the space between us and the light keeps stretching faster than the light can travel through it! So there’s another notional sphere around us at the distance where this starts happening; this is the “cosmic event horizon”. While the particle horizon is the boundary between what we can see already and what we can’t see yet, the event horizon forms a boundary between what we can ever see—if we look hard enough and wait long enough—and what we will never be able to see, no matter how hard we look or how long we wait.

The distance to the cosmic event horizon at a particular time $t$ is given by: $$ d_e(t) \equiv a(t) \; c \int_t^\infty \frac{dt'}{a(t')} $$ Here, as in the previous article, $a(t)$ is the universal scale factor—the function that encodes the expansion of the universe with time—and $c$ is the speed of light. As you can see, the distance to the cosmic horizon depends on the entire future history of the universe, from the time at which we’re evaluating it infinitely far into the future. This is consistent with the idea that it describes how far we can see if we wait long enough.

Unfortunately, the unbounded integral means we can’t apply numerical integration to calculate this value, since we’d have to evaluate $a(t)$ (itself numerically integrated) at arbitrarily large times, which doesn’t sound very tractable. (Although, if you happen to know a trick by which integrals like this can be done numerically, let me know in the comments!) Therefore, I’m going to take a different approach: finding asymptotic solutions for $a(t)$ and then doing the integral analytically.

Let’s recap: last time, $a(t)$ was defined by a differential equation, the Friedmann equation, with three terms: one each for matter, radiation, and dark energy. But the further we go into the future, the less influence matter and radiation have. Dark energy becomes by far the dominant term, so it’s not too bad of an approximation to drop the other two and look at a simplified model with just dark energy, and nothing else. This equation is: $$ \frac{d^2 a}{dt^2} = -\tfrac{4}{3} \pi G \rho_{DE0} (3w + 1) \bigl[ a(t) \bigr]^{-3w - 2}, $$ where $G$ is the gravitational constant and $\rho_{DE0}$ is the present-day density of dark energy—equal to 6.78 × 10⁻²⁷ kg/m³.

I’ll spare you the details of solving this equation and then calculating the distance to the cosmic horizon (although if you really must dig into it, you can look at this appendix). It so happens that there are three cases: $$ d_e(t) = \begin{cases} \dfrac{c}{|3w + 1|} \left[\left(\tfrac{2}{3} \pi G \rho_{DE0}\right)^{-1/2} + |3w + 3| t \right] & \text{if } w > -1 \\[12pt] \dfrac{c}{2} \left(\tfrac{2}{3} \pi G \rho_{DE0}\right)^{-1/2} & \text{if } w = -1 \\[8pt] \dfrac{c}{|3w + 1|} \left[\left(\tfrac{2}{3} \pi G \rho_{DE0}\right)^{-1/2} - |3w + 3| t \right] & \text{if } w < -1 \\ \end{cases} $$

From this equation we can see that $w > -1$ gives a horizon that grows over time; $w = -1$ gives a constant-sized horizon, and $w < -1$ gives a shrinking horizon! In particular, for $w = -0.9$ the horizon is about 19 billion light-years away and is receding at about 17% of lightspeed. For $w = -1.0$ it’s about 16 billion light-years away, and for $w = -1.1$ it’s 14 billion light-years away and approaching at about 13% of light speed. What does this mean?

Recall that $w > -1$ corresponds to dilution of dark energy and slow expansion; $w = -1$ gives constant-density dark energy and faster expansion; and $w < -1$ gives concentration of dark energy and rapid expansion. The position of the cosmic horizon acts as a sort of barometer for dark energy behavior!

As mentioned earlier, in a static, non-expanding universe, we’d eventually be able to receive information about events that occurred anywhere in the universe and at any time. The farther away those events occurred from us, the longer it would take us to know about them because of the limitation of lightspeed, but after waiting long enough we could eventually receive a signal originating from any place and time.

In an expanding universe, there are some places and times—those beyond the horizon—from which no signal could reach us. When $w = -1$ exactly, the horizon is at a fixed distance, and in this case, the fixed volume of space within the horizon is all we’ll ever be able to see. We can never know of any events occurring outside that volume. Moreover, as time goes on, the expansion of space will push all the other galaxies ever farther away…and eventually they will cross the horizon, rendering any later events in those galaxies unknowable to us.

It’s a bit depressing to think that no matter what technology or civilization comes to exist in the future, it would never be able to see more than this fixed volume of space, and would gradually lose contact with all the other galaxies—even though both the volume of space involved and the number of galaxies within it are indescribably vast!

When $w > -1$, the situation is a bit better. In this case, the horizon grows over time, so the volume of space visible to us also grows. Unfortunately, the expansion is already pushing galaxies away faster than the horizon is growing, so just as before, there are many galaxies we will never see—and many more that are visible now but will eventually disappear behind the horizon. However, since the horizon does grow a bit, there is a core volume of galaxies that will not ever leave our horizon. We can look forward to observing (and perhaps communicating with) those galaxies forever.

But the last scenario is positively frightening! When $w < -1$, the horizon closes in on us over time. This is because the concentration of dark energy causes the universal expansion to speed up so much that ever-nearer galaxies will be driven away faster than signals from them can reach us. In both of the other scenarios, the universe lasts forever, although it’ll be lonelier in the far future—but in this case, space-time effectively self-destructs on a certain future date, at which point the density of dark energy and the rate of expansion both become infinite! This is an “end of the world” far more comprehensive and final than anything certain doomsayers have imagined is in store for the Earth in 2012!

This scenario is referred to as the “Big Rip” (because spacetime “rips itself apart”), and if our universe’s destiny includes such an apocalypse, it could occur as soon as 100 billion years from now. But the closer $w$ is to −1, the more slowly the horizon shrinks, and the further in the future is the Big Rip, if it happens at all.

So which scenario best describes our universe? At present, astronomical observations are unable to say, since measurements of $w$ hover right around −1, the cusp between the three cases. Theory is not much help here either: although $w = -1$ is in a sense the simplest case, particle-physics models do exist that implement the other two cases, as well. The truth is that we just don’t yet know enough about particle physics to say with any confidence. A theory of quantum gravity will probably be necessary to answer this question authoritatively!

For more discussion of the cosmic event horizon and various other kinds of horizons in the universe, see this paper. The expansion of the universe really is a deep and fascinating topic, and there’s plenty more that can be said about it than I have in these two articles!