Antialiasing: To Splat Or Not
Note: this post is adapted from an answer I wrote for the Computer Graphics StackExchange beta, which was shut down a few months ago. A dump of all the CGSE site data can be found on Area 51.
To perform antialiasing in synthetic images (whether real-time or offline), we distribute samples over the image plane, and ensure that each pixel gets contributions from many samples with different subpixel locations. This approximates the result of applying a low-pass kernel to the underlying infinite-resolution image—ideally resulting in a finite-resolution image without objectionable artifacts like jaggies, Moiré patterns, ringing, or excessive blurring.
In treatments of this process that I’ve read (such as in PBR) we are told to do this by a method that I’ll call splatting: generating a collection of samples uniformly distributed over the image rectangle, then for each sample, accumulating its color onto all nearby pixels, with weights according to the distance between the sample and the pixel centers (using any desired antialiasing kernel as a falloff function).
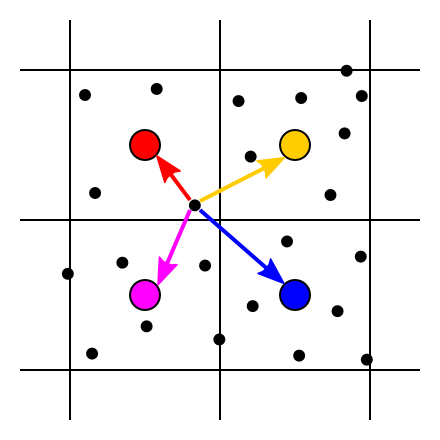
Each sample (small black dot) contributes to several nearby pixels (big colored circles)
I wondered: couldn’t we do this a simpler way? Instead of splatting each sample across all nearby pixels, couldn’t we just generate, for each pixel, an independent set of samples (using any desired antialiasing kernel for the distribution), and have each of those samples contribute only to the individual pixel that generated it?
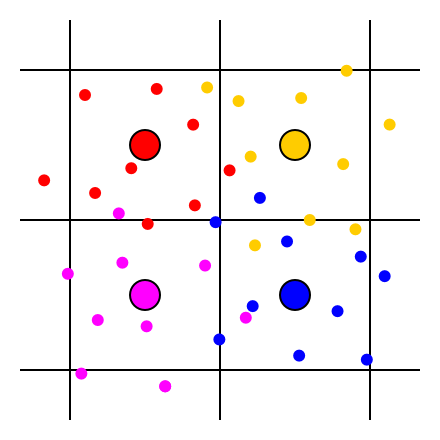
Each pixel (big colored circle) generates several samples (small colored dots) around it; each sample contributes only to the pixel that generated it
Formally, both approaches should converge to the same image in the limit that the number of samples goes to infinity; they both approximate the same low-pass kernel applied to the infinite-resolution image. But using the non-splatting approach would slightly simplify the problem of building an efficient multicore renderer, since the relationship between samples and pixels would be many-to-one instead of many-to-many. I also wondered if there might be image-quality implications—the splatting approach, by reusing samples, introduces potentially-unwanted correlations between nearby pixels.
I asked about this on the then-active CGSE site, but no one had a ready answer, so I decided I had to do some tests of my own. I concocted a simple 2D mathematical function with a wide range of frequencies (to stand in for rendering a scene), and wrote a program to evaluate and filter it, using a few different kernels, with either the splatting or the non-splatting method as defined above. I found some interesting results.
The Test
For reference, my source code is here—Python 3.4 with Pillow and numpy. This is purely intended to test image quality, not performance. And I’m not even measuring the image quality scientifically—just eyeballing it.
To start with, here’s the image I’m sampling. (BTW, it may help to open these images in a new tab, or download and view them in an external program, to ensure your browser isn’t resizing them and doing something weird.)

The function has infinitely-sharp edges between the black and white bands, and the spatial frequency of the edges is low near the bottom of the image and increases toward the top. This image was generated with one million samples per pixel and a 2px-radius Lanczos filter, so I figure it’s about as close to a perfectly filtered image as you’re going to get, although it still shows some aliasing in the midrange frequencies.
(By the way, I also tried a 3px Lanczos filter, but it gave very visible ringing around the edges in the lower half.)
Here’s the same function, evaluated with just one measly sample at each pixel center, no attempt at antialiasing:

All sorts of jaggies and Moiré patterns, as you’d expect.
Box Filter
Okay, now for the interesting part. Here’s the function evaluated with just 16 samples per pixel using the splatting method with a 2px-radius box filter (so 4px diameter; I’m deliberately using a wider filter here than you’d use in real life, to exacerbate the effects).
Note that for the splatting method, when I say “16 samples per pixel” I mean that the total number of samples was 16 times the number of pixels in the image. However, because each sample splats onto multiple pixels, the number of samples contributing to any individual pixel is more than 16.

And here’s the non-splatting method, with the same parameters. Here, each pixel received contributions from exactly 16 samples, distributed in a 2px-radius box around the pixel center.

Comparing these two, we can see several interesting features:
- The overall noise amplitude in the upper part of the image is about the same between the two methods.
- However, the noise frequency is quite different! Without splatting, you get high-frequency noise because each pixel’s samples are totally independent. With splatting, the samples used for nearby pixels are correlated (in other words, the noise is filtered by the antialiasing kernel), so you get lower-frequency noise.
- The aliasing of the midrange frequencies that are not properly filtered looks about the same between the two methods.
- In the lower part of the image, the filtered edges look quite smooth (albeit blurry) with splatting, but rather noisy without. This is presumably due to the greater number of contributions per pixel from sample reuse when splatting.
Gaussian Filter
In a real rendering task, you probably wouldn’t use a box filter, as there are much better choices available! Let’s take a look at what happens with a Gaussian filter with sigma = 0.5px (total radius 3 sigma, or 1.5 px), again with 16 spp. Splatting:

And non-splatting:

The comparison is qualitatively very similar to the box filter: again, splatting gives lower-frequency noise in the upper part and better-filtered edges in the lower part. This Gaussian is actually a rather nice filter that you might use in real life; it’s a good balance between maintaining sharpness and fighting aliasing.
Lanczos Filter
There’s just one more comparison I want to make, and that’s with a Lanczos filter. Splatting:

And non-splatting:

Here the result is a bit different! The noise frequency doesn’t look much lower with splatting (due to the sharpening properties of the Lanczos filter?) but the noise amplitude is clearly lower—the opposite of what happened before.
I’m not entirely sure what’s going on here, but it may be due to the fact that the Lanczos filter can’t easily be importance-sampled. For the box and Gaussian filters, in the non-splatting case I generated samples that were distributed to match the filter, and therefore all weighted evenly. For the Lanczos filter, this is a great deal more difficult and I didn’t attempt it, so I just generated uniform samples and weighted them by the kernel. This is well-known to increase variance, and may account for the increased noise in the non-splatting image. Splatting doesn’t have this issue, since it simply evaluates the kernel between sample points and pixel centers—no importance-sampling needed.
After considering these comparisons (and more) I’m coming down on the side of splatting—PBR was right after all! :) It’s a bit more complicated to code, and probably slightly slower when it comes to accumulating samples—but it seems to consistently give higher-quality images for a given sample count, and it’s friendlier to non-importance-sampleable filters like Lanczos. In a renderer of any sophistication, the bottleneck is going to be the per-sample lighting evaluation, not accumulating samples on the image—so anything that gets you better image quality per sample is a win.
Update: Matthäus Chajdas brought to my attention a paper on this topic, Filter Importance Sampling, from 2006. They propose the same “non-splatting” method that I used here—independent samples per pixel, distributed according to the desired antialiasing kernel—but they went ahead and did (approximate) importance sampling for any kernel, including ones with negative lobes such as Mitchell and Lanczos.
They find that in the presence of additional random sampling in the generation of the image (light sampling, BRDF sampling, etc.) the non-splatting method produces better images, due to weighting each sample equally. The splatting method can increase variance because, for example, a sample with a large light value can end up with a high weight in one pixel and a low weight in the next pixel, producing fireflies.
So it seems that my test case was too simplistic, and using a function that can be exactly evaluated as a stand-in for rendering an image leads to a different conclusion from actually rendering an image!